Animation / simulation
Keyframe Animation 关键帧动画
画师画出关键的画面,再由其助手补全关键帧之间的过渡
所以关键帧动画的主要问题在于使用怎样的插值方法得到更为平滑的过渡
通常来说线性插值是无法满足平滑过渡的需求的,所以一般会用贝塞尔,b样条之类的几何插值技术
Physical Simulation 物理模拟
通过建立物理模型来还原诸如流体,布料等基于真实情况的动画
Mass Spring System 质点弹簧系统
理想弹簧没有初始长度,且满足牛顿第三定律,用胡克定律求解作用力的大小
在理想弹簧的基础上引入原长,就变成了非零长弹簧
不考虑能量损失,非零长弹簧会始终保持运动的状态
如果简单引入摩擦力,则所有运动最后都会停止
无法考虑弹簧内部的相互作用力的影响 再引入一个内部的阻尼力
最终得到:

红框内表示b与a的相对速度在二者连线方向上的投影,是一个标量,再乘以b到a的归一化方向以及劲度系数,就得到的b上的总阻力
两个质点->弹簧系统,模拟纸或布料这种具有抗切变性质的材质
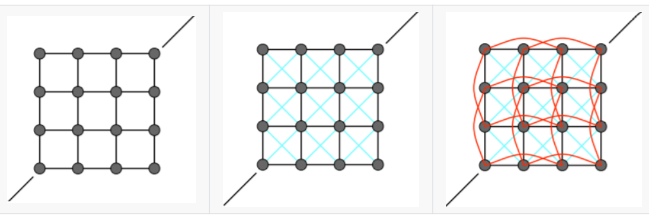
抗切变:对于平面内的力,普通质点弹簧系统一拉就会变形,而抗切变材质不会;对于非平面力,质点弹簧系统可以做到完美对折,而抗切变材质不会
为了模拟这种情况,对原本的质点弹簧系统添加两步约束,如上图所示,一个是对角线的强约束,一个是跨顶点的弱约束
依旧不够精确Particle Systems 粒子系统
粒子生成的步骤如下:
生成粒子 -> 计算每个粒子的力 -> 更新每个粒子的位置和速度 -> 将死亡的粒子移除 -> 渲染到屏幕
粒子之间常见的作用力举例:重力,电磁力,摩擦力,空气阻力,粘滞力,碰撞等
粒子的模拟不仅限于计算机图形,现实中的大自然如鸟群行为,细胞结构都可以通过粒子模拟Kinematics 运动学
正向运动学 Forward Kinematics 是通过定义一些可活动关节(如铰链),通过计算来控制末端的点的运动
逆向运动学 Inverse Kinematics 是艺术家习惯直接控制末端的点的运动,而不是控制关节来间接运动
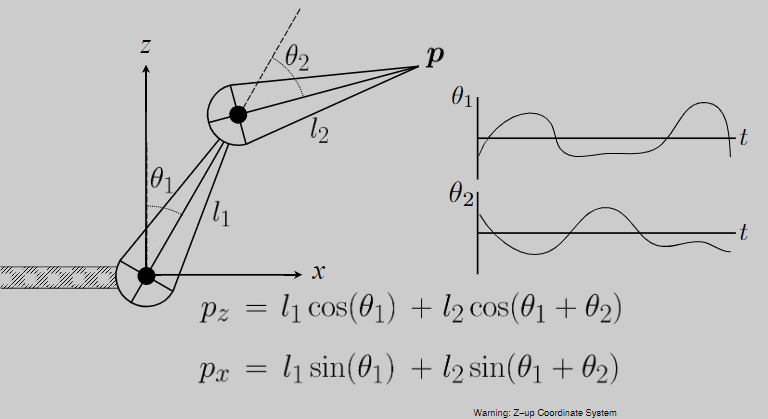
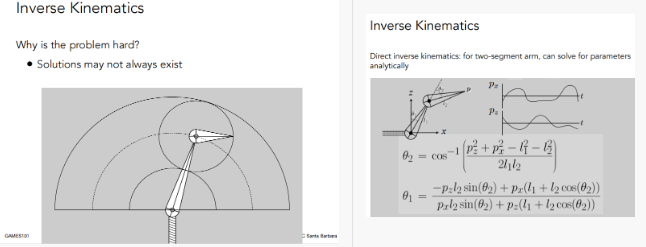
Rigging 角色绑定
形象理解为提线木偶,是对逆运动学的一种应用
角色的动作与动作之间原本需要对三维模型进行插值,现在只需要对骨骼插值即可Motion Capture 动作捕捉
捕捉真实的控制点来生成动画
光学动捕,在动捕演员的关键位置设置信号源,还有诸如应用了电磁波的或是直接纯机械的动捕,都可以达到最终目的The Production Pipeline
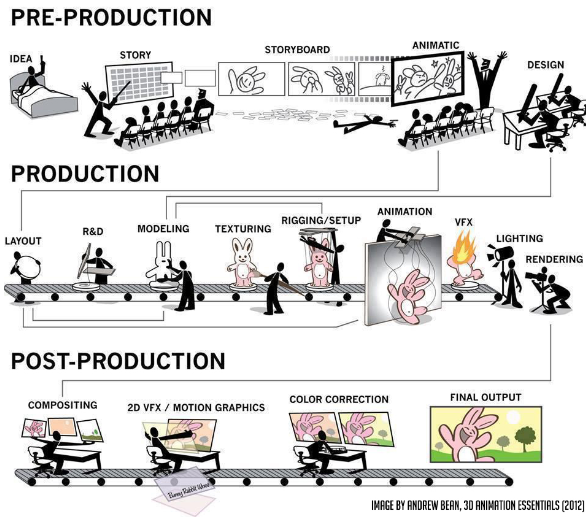
模拟方法
Single particle simulation 单粒子模拟
模拟一个粒子的运动 假定一个速度场,在场内使用一阶常微分方程来得到其速度信息 计算得到速度之后,再用欧拉方法等各种手段,解出位置信息,得到模拟结果
Euler’s Method
对时间进行离散化,以一定步长细分时间,并每次用前一帧的计算结果更新当前帧的位置信息(前项欧拉)
前项欧拉 $x^{t+\Delta t} = x^t + \Delta t \dot{x}^t$
非前项欧拉 $\dot{x}^{t+\Delta t} = \dot{x}^t + \Delta t \ddot{x}^t$
不过,这么做容易造成很大的误差,并且稳定性也非常差
一旦步长低于一定精度,这种模拟就显得非常粗糙 在一些速度场中,产生的误差会被无限放大,出现正反馈现象Combating Instability
Midpoint Method 中点法
做了两次欧拉方法,第一次欧拉方法获得中点位置,在取中点位置的速度,再代入算一遍欧拉方法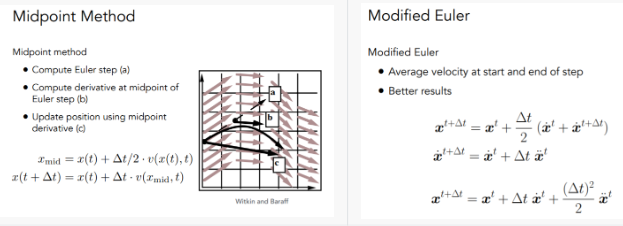
Adaptive Step Size 自适应步长方法
也是算两遍欧拉,第一遍用$\Delta t$算,第二遍用$\frac{\Delta t}{2}$算,算完之后检验两次计算结果,如果偏差较大,则步长减半重新计算
这与直接减小步长的最大差别就是,他可以根据计算结果判断哪里应该用小步长,哪里用大步长,这就是所谓的“自适应”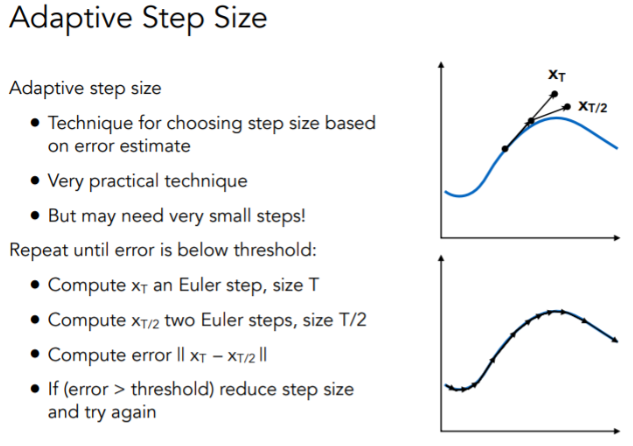
Implicit Euler Method 隐式欧拉方法
又称后向欧拉方法,前向欧拉是每次计算都用前一帧数据,那后向计算顾名思义就是用未来的数据
需要求解非线性方程组,会用到牛顿法等求根算法,计算会慢,但稳定性相应也高 一阶稳定
Runge-Kutta Families
一种四阶的方法,稳定性非常好
Position-Based / Verlet Integration 非物理方法
如位置调整法,韦尔莱积分等 通过调整粒子的位置使其满足一些特定性质
Rigid body simulation 刚体模拟
刚体不会发生形变,并且内部所有粒子都以同一种运动方式运动
那么相对于粒子模拟只考虑位置和速度,刚体模拟会考虑更多的参数,如角度和角速度,角速度和角加速度等这些的对应关系
Fluid simulation 流体模拟
流体模拟同样认为流体粒子不可压缩,且密度处处相等(变化前后密度也保持不变),那么任何时
刻,任意位置的流体粒子发生运动都会导致其周围粒子的密度发生变化(马尔科夫链),而要使运动前后密度不变,就需要通过改变流体粒子位置来修正
有两种主流的模拟思想,拉格朗日视角(质点法)和欧拉视角(网格法)
前一种是逐个进行单粒子模拟,后一种是将空间定义为多个网格单元,通过观察网格来决定如何模拟
将上述两种思想结合,就是现在流行的材质点方法(MPM)
具体做法是,先将属性参数储存在粒子上(拉格朗日视角),再在模拟变换的过程中运用欧拉视角进行模拟计算,最后将每一个时刻网格的信息写回网格内的粒子上,并渲染到屏幕上

