Unity Shader 入门精要

Materials

Material

Material == BRDF
BRDF 描述单位受照面吸收能量后辐射出去的Radiance分布情况 就表示了材质如何与光线作用

Diffuse / Lambertian Material 漫反射材质

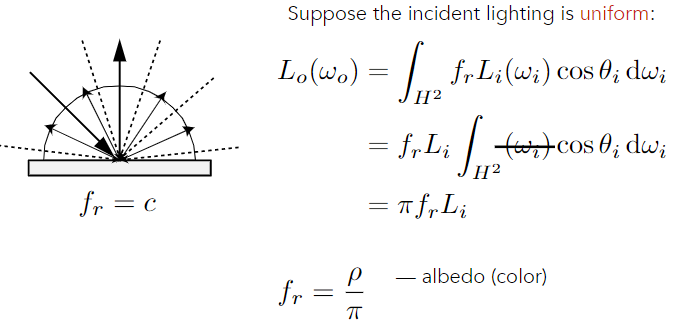
不同于经验性的blinn-phong模型用 Intensity/R² 来不准确地定义到达着色点的能量
由渲染方程(假设任意方向的入射光和出射光的Radiance和Irradiance都相等，着色点不吸收任何能量，且自发光项为0)推出的$f_r$以及定义的albedo反射率相乘可以控制材质颜色变化 引入反射率ρ，取值0~1让物体能够接受能量获得不同颜色的BRDF

Glossy material (BRDF)光泽材质

介于漫反射和镜面反射之间 光线反射集中在一个小范围内

Ideal reflective / refractive material (BSDF*) 理想反射/折射材质

光线到达材质表面被吸收一部分，同时发生镜面反射和镜面折射

• Perfect Specular Reflection
  
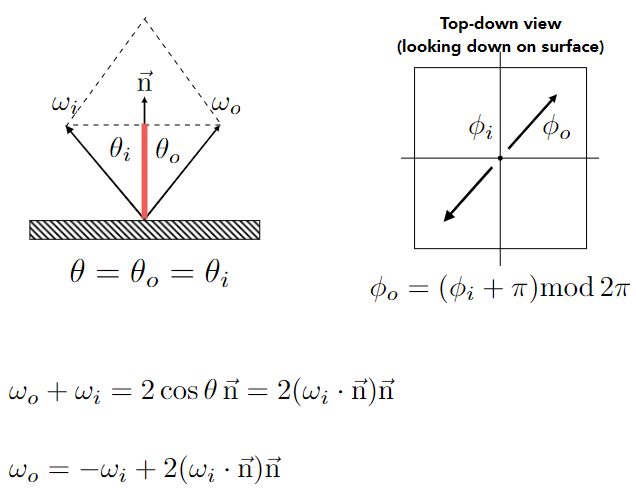
  左图（正视图）观察入射角和出射角，右图（俯视图）观察方位角

• Specular Refraction
  Snell’s Law $\qquad n_i\sin\theta_i = n_t\sin\theta_t$
  可推得
  
  
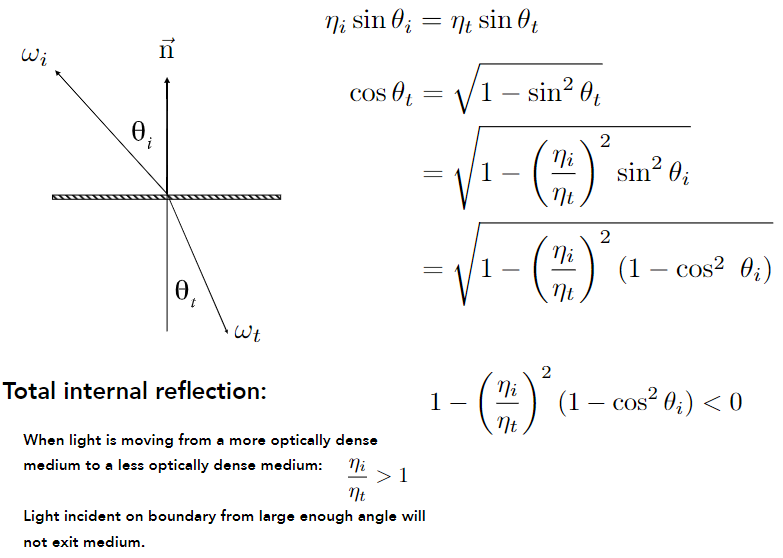
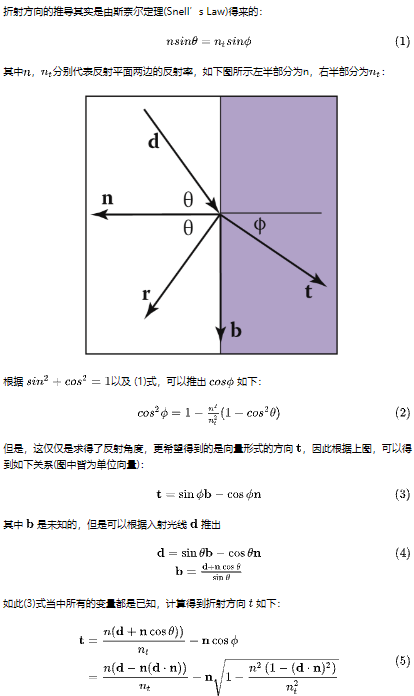
  对于$\cos\theta$中根号项 需要保证大于0才能发生折射
  入射材质的折射率大于出射材质折射率时观察角度足够大会全反射

  • Fresnel Reflection
    物体的反射率其实与你的观察角度即有关，对于绝缘体来说观察角度与法线夹角越大，反射的程度就越大
    在相同的入射角情况下，不同的材质也具有不同的反射率，即具有不同的菲涅尔项
    计算精确的反射率
    
    物体的反射率和入射角度，和入射空间的折射率，和物体的折射率有关
    下半部分为近似结果

• 双向散射分布函数(BSDF)
  描述反射的分布函数被称为双向反射分布函数（BRDF），那么描述折射也需要一种分布函数
  这种分布函数被称为双向折射(透射)分布函数（BTDF）
  BRDF和BTDF统称为双向散射分布函数（BSDF）
  $f_s=f_r+f_t$

Microfacet Material

离得足够远的时候，微观表面可以被忽略，而最后看到一个宏观的结果

• 微观解释镜面反射 漫反射:
  法线方向分布比较集中的镜面反射明显，而法线分布比较分散表面相对粗糙
  
  从微观看漫反射表面，每个微元表面都是完美镜面反射 当光线照射到物体表面时，一部分光线会与表面的许许多多的微小镜面发生镜面反射，另一部分光线则会折射进入物体内部
  光线折射进入内部的时候会与物体的微小粒子不断发生碰撞并散射到随机方向，同时在碰撞的过程中一部分光线的能量会被吸收转换为热能，有些光线在多次碰撞之后能量消耗殆尽，则表示该光线完全被物体吸收。还有一部分折射到物体内部的光线会因为散射方向的随机性重新离开表面，而这部分光线就形成了漫反射
  (不考虑光线散射出来离开表面的点可能并不是进入表面的点这种情形，次表面散射(Subsurface Scattering)技术考虑了 可见AdvancedTopics中半透明材质BSSRDF)
  漫反射和次表面散射其实是相同物理现象，本质都是折射光的次表面散射的结果。唯一的区别是相对于观察尺度的散射距离 光的折射现象，建模为漫反射还是次表面散射，取决于观察的尺度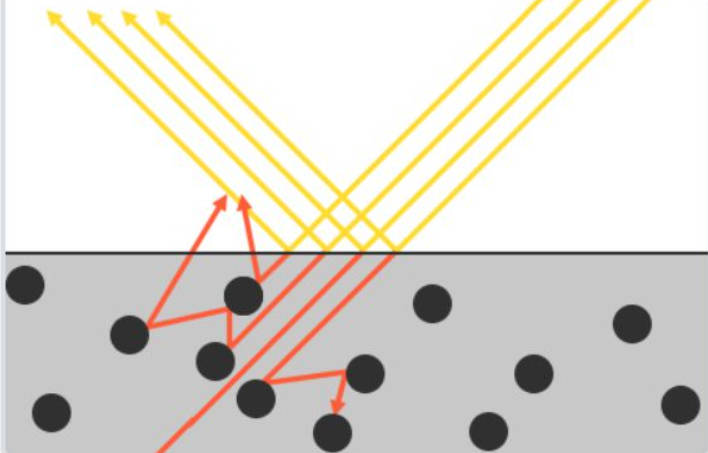
  

有了微表面模型，我们就可以提出在微表面下的更精确的BRDF方程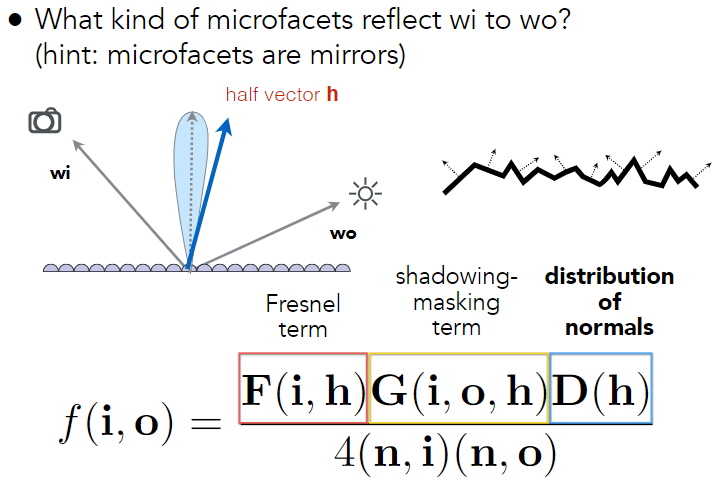

• F为菲涅尔项；描述了物体表面在不同入射光角度下反射光线所占的比率
• D为法线分布函数，查询半程向量是否在法线分布内
• G为几何项，由于在微表面上，对于那些几乎和表面平行的入射光，很容易发生互相遮挡的现象，从而使得部分微表面失去作用，我们把这种光线角度称为掠射角度（Grazing Angle），在这种角度下的着色会非常亮，G项就起到了一定的修正作用

微表面模型可以得到非常真实的渲染结果，因为他本身就是基于物理的渲染（PBR/PBS）

以上为仅考虑微观镜面反射时的情况, 折射会造成能量损失, 所以很多模型会增加某一项去补回能量的损失.如 cook-torrance微表面模型, Kulla-Conty 模型(见RTR-PBR)

Isotropic / Anisotropic Materials (BRDFs)

各向同性（Isotropic Materials）：微表面不存在方向性
各向异性（Anisotropic Materials）：微表面存在方向性 不锈钢,尼龙,天鹅绒
对BRDF 方向性是指如果入射光和出射光做一定方位角的旋转前后，BRDF方程不变

Properties of BRDFs

Non-negativity 非负性：描述能量分布
Linearity 线性性：可以被拆分成不同项的线性组合（ambient，diffuse，specular)
Reciprocity principle 可逆性：调换入射出射方向，BRDF渲染结果严格不变
Energy conservation 能量守恒：出射光线的能量永远不能超过入射光线的能量
Isotropic vs. anisotropic 各向同/异性：如果是各项同性材质，则BRDF值只和相对方位角有关，四维的BRDF材质可以被降维为三维，并且根据可逆性，结果不需要考虑方位角的正负

Measuring BRDFs

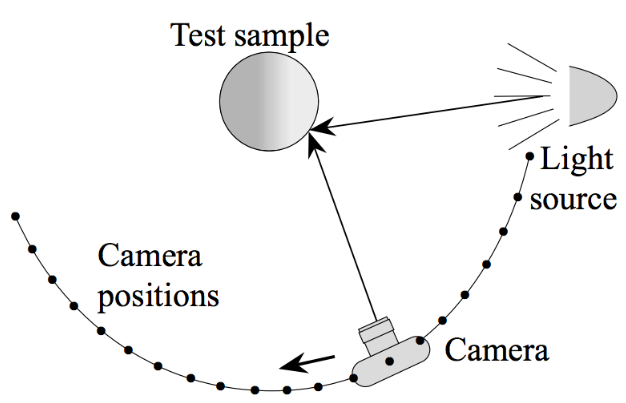
给定一个着色点，通过改变入射和出射的角度（改变光源与相机位置）进行测量

foreach outgoing direction wo
    move light to illuminate surface with a thin beam from wo
    for each incoming direction wi
        move sensor to be at direction wi from surface
        measure incident radianc

这样测出来的BRDF是四维的，这样的测量是非常费时的
为了提高效率，我们可以尽量让材质呈各向同性
就像之前说的，这不仅可以让BRDF从四维降至三维，还能由光路可逆性再砍去一半的测量

Advanced Appearance Modeling 高级外观建模方法

• Non-surface models
  • Participating media 散射介质
  • Hair / fur / fiber (BCSDF)
  • Granular material 颗粒材质
• Surface models
  • Translucent material (BSSRDF) 半透明材质
  • Cloth
  • Detailed material (non-statistical BRDF)
• Procedural appearance 程序化生成材质