Unity Shader 入门精要

Transformation 基础变换

Linear Algebra

Dot product

$$\vec{a}\cdot\vec{b} = \big\lvert \lvert a \rvert \lvert b \lvert \big\rvert \cos \theta\\ \cos \theta = \hat{a}\cdot\hat{b}\\ \vec{a}\cdot\vec{b} = \binom{x_a}{y_a} \cdot \binom{x_b}{y_b} = x_ax_b + y_ay_b$$

求投影projection
求夹角
判断前后

Cross product

$$\vec{a}\times\vec{b} = \left( \begin{matrix} y_az_b-y_bz_a \\ z_ax_b-x_az_b \\ x_ay_b-y_ax_b \end{matrix} \right)\\ \vec{a}\times\vec{b} = A*b = \left( \begin{matrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{matrix} \right) \left( \begin{matrix} x_b \\ y_b \\ z_b \end{matrix} \right)$$

判断左右和前后
右手系$\vec{\omega}=\vec{u}\times\vec{v}$

Matrices

$$(M\times N)(N\times P) = (M\times P)$$

不满足交换律 满足结合律

转置Transpose

$$\left( \begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix} \right)^\mathrm T= \left( \begin{matrix} 1 & 3 & 5\\ 2 & 4 & 6 \end{matrix} \right)$$

2D transformations

Linear Transforms:
用相同维度的矩阵相乘进行变换
Scale Matrix

$$\left[ \begin{matrix} x' \\ y' \end{matrix} \right]= \left[ \begin{matrix} s_x & 0 \\ 0 & s_y \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right]$$

Reflection Matrix

$$\left[ \begin{matrix} x' \\ y' \end{matrix} \right]= \left[ \begin{matrix} -1 & 0 \\ 0 & 0 \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right]$$

Shear Matrix

$$\left[ \begin{matrix} x' \\ y' \end{matrix} \right]= \left[ \begin{matrix} 1 & a \\ 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right]$$

Rotation Matrix 默认逆时针

$$\left[ \begin{matrix} x' \\ y' \end{matrix} \right]= \left[ \begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right]$$

3D Transforms

3D Rotations
我们所采用的是右手系，在二维之中其逆时针旋转矩阵是x轴向y轴旋转，对应到3维便是绕z轴旋转(x轴转向y轴)，不难推出绕x轴旋转(y转向z)，绕y轴旋转(z转向x)

$$R_x(\alpha)= \left( \begin{matrix} 1 & 0 & 0 & 0\\ 0 & \cos\alpha & -\sin\alpha & 0\\ 0 & \sin\alpha & \cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right)\\ R_y(\alpha)= \left( \begin{matrix} \cos\alpha & 0 & \sin\alpha & 0\\ 0 & 1 & 0 & 0\\ -\sin\alpha & 0 & \cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right)\\ R_z(\alpha)= \left( \begin{matrix} \cos\alpha & -\sin\alpha & 0 & 0\\ \sin\alpha & \cos\alpha & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right)\\$$

任意旋转矩阵都是正交矩阵($AA^T=I$) 正交矩阵逆和转置相同 $R_{-\theta} = R_\theta^T$

(所有的旋转都是针对原点来说)

Affine Transformations仿射变换

• Homogeneous coordinates 齐次坐标

  引入齐次坐标目的:将平移也用矩阵变换实现

  $$\left[ \begin{matrix} x' \\ y' \end{matrix} \right]= \left[ \begin{matrix} a & b \\ c & d \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right]+ \left[ \begin{matrix} t_x \\ t_y \end{matrix} \right]$$

  添加一个维度

  $$\left[ \begin{matrix} x \\ y \\ \omega \end{matrix} \right]$$

  $\omega$为0时表示矢量 不为0时表示点
  且为点时

  $$\left[ \begin{matrix} x \\ y \\ \omega \end{matrix} \right]和 \left[ \begin{matrix} x/\omega \\ y/\omega \\ 1 \end{matrix} \right]表示一个点$$

  vector + vector = vector
  point - point = vector
  point + vector = point
  point + point = point(中点)

仿射变换

$$\left[ \begin{matrix} x' \\ y' \\ 1 \end{matrix} \right]= \left[ \begin{matrix} a & b & t_x\\ c & d & t_y\\ 0 & 0 & 1 \end{matrix} \right]\cdot \left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right]$$

3D同2D增加一个维度

$$\left[ \begin{matrix} x' \\ y' \\ z' \\ 1 \end{matrix} \right]= \left[ \begin{matrix} a & b & c & t_x\\ d & e & f & t_y\\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{matrix} \right]\cdot \left[ \begin{matrix} x \\ y \\ z \\ 1 \end{matrix} \right]$$

先进行线性变换再平移变换

最后一维为1，表示点(point), 为0表示方向(direction).方向的位移没有意义，方向始终不会变。第四维不是只能是1和0，在投影变换中，齐次坐标会有更多的作用

Composing Transforms组合变换

不满足交换率 从后往前实现
满足结合率
对绕非原点的旋转可先平移再绕原点旋转再平移回去

Viewing Transformation 观测变换

将虚拟世界中以(x,y,z)为坐标的物体变换到 以一个个像素位置(x,y) 来表示的屏幕坐标系之中(2维)
Think about how to take a photo (MVP)

• Find a good place and arrange people (model transformation)游戏场景中的物体调整至他们应该在的位置
• Find a good “angle” to put the camera (view transformation)得到物体与摄像机的相对位置
• Cheese! (projection transformation)将三维空间投影至标准二维平面($[-1,1]^2$)之上(这里的z并没有丢掉，为了之后的遮挡关系检测）
• 视口变换(viewport transformation)：将处于标准平面映射到屏幕分辨率范围之内，即$[-1,1]^2→[0,width]*[0,height]$, 其中width和height指屏幕分辨率大小

View / Camera Transformation 视图变换

Define the camera first

• Position $\vec{e}$
• Look-at / gaze direction $\hat{g}$
• Up direction $\hat{t}$

transform the camera to The origin, up at Y, look at -Z 相机和物体一起都要变换

正常旋转不好就考虑逆变换 旋转矩阵的逆变换既为转置

Projection Transformation 投影变换

Orthographic projection 正交投影

simple:
Drop Z coordinate
Translate and scale the resulting rectangle to [-1, 1]

In general:
将物体全部转换到一个$[−1,1]^3$的空间之中
将原空间范围的左下角移至原点 放大给定倍数 将缩放后的空间范围移至新空间范围

$$M_{ortho}= \left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{matrix} \right]= \left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f}\\ 0 & 0 & 0 & 1 \end{matrix} \right]$$

摄像机方向:看向z的负方向 所以远的物体z更小

Perspective projection 透视投影

看成先挤压为长方体再正交投影

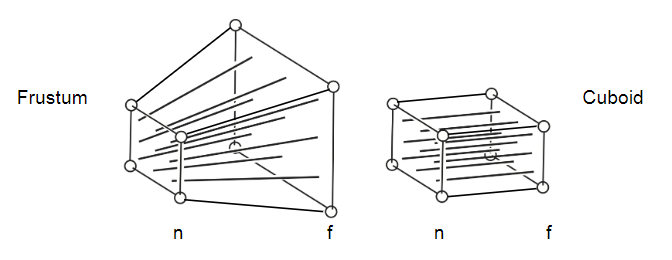
$y’=\frac{n}{z}y$ x同y

$$M_{persp->ortho} \left( \begin{matrix} x \\ y \\ z \\ 1 \end{matrix} \right)=> \left( \begin{matrix} \frac{n}{z}x \\ \frac{n}{z}y \\ unknown \\ 1 \end{matrix} \right)== \left( \begin{matrix} nx \\ ny \\ unknown \\ z \end{matrix} \right)$$

再由两个特殊点，近平面z=n上的点不变和远平面z=f上的点的z坐标不变可得矩阵

$$\left( \begin{matrix} 0 ,0 ,A ,B \end{matrix} \right) \left( \begin{matrix} x \\ y \\ n \\ 1 \end{matrix} \right)=>n^2 \qquad \left( \begin{matrix} 0 ,0 ,A ,B \end{matrix} \right) \left( \begin{matrix} x \\ y \\ f \\ 1 \end{matrix} \right)=>f^2$$ $$M_{persp\rightarrow ortho}= \left( \begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{matrix} \right)\\ M_{persp}=M_{ortho}M_{persp\rightarrow ortho}= \left[ \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{l-r} & 0\\ 0 & \frac{2n}{t-b} & \frac{t+b}{b-t} & 0\\ 0 & 0 & \frac{n+f}{n-f} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0 \end{matrix} \right]$$

以上得到$[-1,1]^3$

详细推导: https://zhuanlan.zhihu.com/p/122411512?utm_source=qq&utm_medium=social&utm_oi=605668290971045888

viewport transformation 视口变换

$[-1,1]^2→[0,width]*[0,height]$ 三维变二维

$$M_{viewport}= \left( \begin{matrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right)$$

$M=M_{viewport}M_{persp}M_{view}$

变换法线向量

模型变换可能会导致模型位置形状发生改变，如果属于该模型的各个三角形面的法线向量不跟着改变的话，那么此时所记录的法线向量就是错误的。因此法线向量一定也要跟着模型本身发生改变
对模型实行M矩阵的变换之后:

1. 平移, 旋转的情况下，法线变换矩阵就是变换矩阵M，不需要额外计算；
2. 等比缩放情况下，法线变换矩阵就是变换矩阵M，法线变换后需要除以缩放比例归一化；

3. 其他情况使用$N = (M^{-1})^T$求法线变换矩阵

   n为法向量 t为切向量 $t_M$为变化后的切向量 $n_N$为变化后的法向量
   $n^Tt = n^TIt = n^TM^{-1}Mt = 0$
   $(n^TM^{-1})Mt = n^TM^{-1}t_M = 0$
   $n_N^T = n^TM^{-1}$
   $n_N = (n^TM^{-1})^T = (M^{-1})^T n$

   M不可逆时使用伴随矩阵$A^ = |A|A^{-1}$ $N = (M^)^T$

详细推导 https://zhuanlan.zhihu.com/p/449976247