Shadows
Shadow Mapping
实现硬阴影
A 2-Pass Algorithm 两趟的算法 第一趟从光源看生成shadowmap 第二趟从照相机看
OpenGL: 1-pass在light处放置一个相机,然后往某一方向看去,定义framebuffer写到某个texture上,然后在fragment shader中定义写的是一个深度而非shading的结果,在2-pass中则只需要用1-pass得到的texture即可
真正生成阴影时比较两个pass中的depth时需要一致,要么都用投影后的Z值比较,要么通过两点的位置得一向量算实际距离
cons: 任何一帧都知道物体位置,阴影都是重新算的,shodow map也是重新算的,和物体运不运动无关
issues:
- Self occlusion 自遮挡
shadowmap上一个值对应的一块区域的深度 记录的深度是不连续的,是一个一个像素的深度值组成的 眼睛观察到的像素会误认为深度在前面的像素后面,形成遮挡,即在第二个pass比较深度的时候,shadow map中的深度可能会略低于物体表面的深度,部分片元就会被误计算为阴影 垂直照的时候问题最小,掠射角度grazing angle时问题最大
solution:
添加一个bias (不是常数)去调节自遮挡现象
具体方式就是当一个点深度大于记录深度的值超过一个阈值时,才认为这个点在阴影内(工业)
但会发生偏移 脚后面的阴影被舍弃了 即detach shadow
OpenGL解决: 通过glPolygonOffset来设置偏移量,入射角越大,偏移量越大
学术界解决 Second-depth shadow mapping
即在第一个pass时,渲染一张light看到最近深度的图同时渲染一张次近的图(透过最近的深度的像素再渲染一张最近深度),将两个深度的中间深度来算遮挡阴影 但物体必须watertight且开销大 - Aliasing
shadow map有分辨率,自然会走样
采用级联阴影(CSM),通过牺牲一些显存来对阴影进行分级,从而提高阴影质量
- Self occlusion 自遮挡
Shadow mapping 后的数学原理
实时渲染里的常用约等式
$\int_\Omega f(x)g(x) dx \approx \frac{\int_\Omega f(x) dx}{\int_\Omega dx} \cdot \int_\Omega g(x) dx$
当g的积分的范围很小的时候或者g这个函数足够光滑的时候就会比较准确

把the rendering equation拆开 式子变成左边是visibility(遮挡)右边是shading
适用范围:- 积分范围(积分域)小的情况 如只有一个点光源和方向光源
- 光源的radiance恒定 情况
- 右边的函数足够光滑情况 如brdf是diffuse
- 环境光因为是近似,也能强行使用
Percentage closer soft shadows(PCSS) 软阴影
光源不为点 部分遮挡时产生软阴影
Percentage Closer Filtering (PCF)
早先是用来anti-aliasing而不是softshadows 后续发现可以用作软阴影发展成PCSS
不是对最后已经有锯齿的阴影做模糊
也不是直接filtering shadowmap 会造成阴影和物体交界直接糊起来 而且在第二个pass上做深度测试还是非0即1的结果
而是Filtering the results of shadow comparisons 对visibility(遮挡的结果)平均 把周围像素深度比较的结果加起来平均一下,就得到一个不是非零即一的数
PCSS
filtering size large->越模糊->softer 足够大则能实现软阴影
不同位置的filtering size不同 与接受投影的位置和遮挡物blocker的距离有关 前实后虚
Filter size <-> blocker distance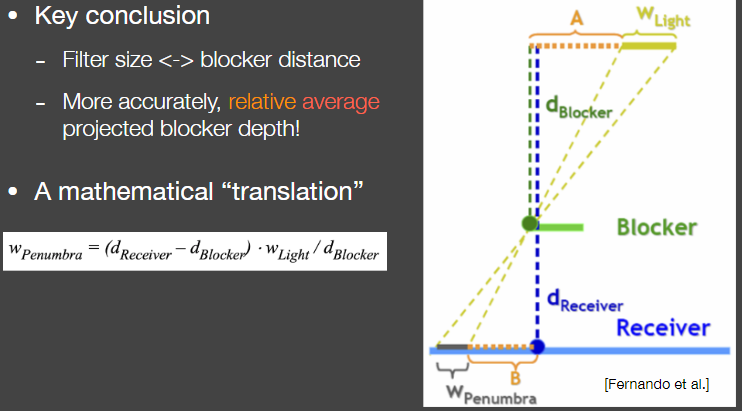
由相似三角形 filtering的范围大小可以通过遮挡物到被遮挡面的距离除以遮挡物到光源的距离乘以光源面积得到 (面光源不会生成shadowmap 一般取光源中间某一点看作点光源生成)
PCSS算法流程
- Blocker search
getting the average blocker depth in a certain region 先搜索一个范围内哪些像素是遮挡物,把这个范围所有遮挡物的深度记下来取个平均值 得到dblocker - Penumbra estimation
use the average blocker depth to determine filter size 算filtering的范围 Percentage Closer Filtering
算pcf 把任意一点p周围一圈texels是否形成遮挡进行加权平均Blocker search
首先找到shading point在shadow map上的点 然后在shadow map对应像素周围区域里面每一个像素存的深度信息与shading point实际的深度比较 区域内的哪些像素存储的深度值比shading point的小,然后用里面这多个像素里面存储的值(就是 d blocker,光源到遮挡物的距离)的平均值average blocker作为真正的dblockerBlocker search 寻找的范围
要么自定义一个范围如4*4 要么如下计算
把shader point连向light,看在shadow map所占范围来确定,因为离光源越远,遮挡物也会更多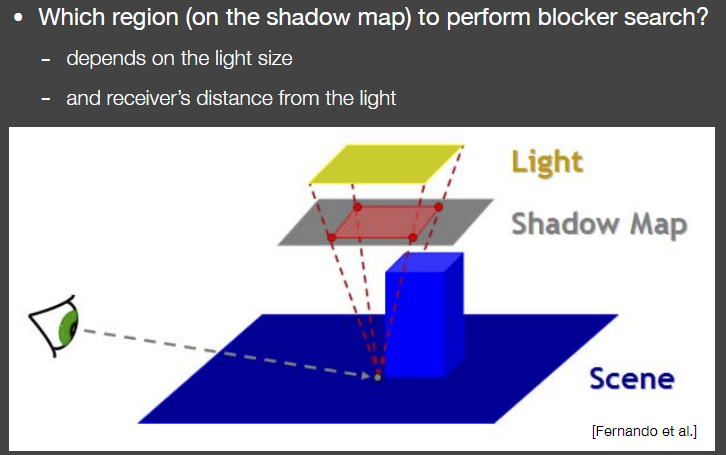
- Blocker search
多光源只能一个一个处理
第一步和第三步比较慢 都要采样整个区域的深度还要进行比较
可以通过随机采样其中的texels,而不全部采样,当然也会造成出现噪声的结果。工业的处理的方式就是先稀疏采样得到一个有噪声的visibility的图 再在图像空间进行降噪(降噪见RTRT)
Variance Soft Shadow Mapping(VSSM)
解决PCSS第一步和第三步慢
第三步:
PCF要和周围一圈进行深度比较得出是否被遮挡,进一步就可以理解成有多少texels比取的点深度浅或深度深 要知道一个人的成绩排多少,就要知道全班人的成绩,这就是之前PCF的做法
可以通过值方图得到一个相对精确的排名,可以当做一个正态分布,正态分布就只需要方差和平均值就能得出 找深度在所有深度中排百分之几生成正态分布:
- 找平均值:
- mipmap
对shadowmap做MIPMAP是做插值,只能在正方形中 在矩形的情况都会有不准 - Summed Area Tables (SAT)
前缀和 范围内求平均
一维把原本的数进行累加,让SAT的每个数都是原本的数从左到当前这个数的总和。这样求某个区域的和时,只要把该区域在SAT中最后一个数减去该区域前的一个数
二维预计算一张从左上角加到右下角的值,这样通过加减的方式,只要采这张图采四次就能得到任意区域的和。这样的结果很准确,但需要O(n(所有元素的个数))的时间和存储
即通过建立m行中每行的SAT和在每行的sat基础上再建立n列中每列的SAT,最终可以获得一个2维的SAT因此最终的SAT,由于gpu的并行度很高,行与行或列与列之间的sat可并行,因此具有m×n的时间复杂度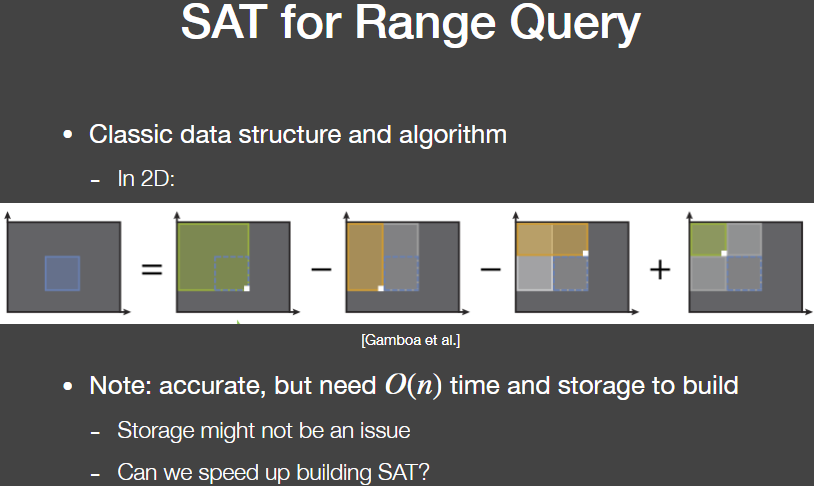
- mipmap
找方差:
$Var(X) = E(X^2) − E^2(X)$
需要额外一张shadermap(深度的平方)得到正态分布 求曲线下的面积 得出有多少texels深度比索取的点小
求面积:
对于通用的高斯的PDF(概率密度函数),可以把积分的值打成表,积分的值就是误差函数(error function)。这个积分没有解析解,只有数值解,c++有个内置函数就是erf就能做CDF(累积分布函数 是概率密度函数的积分)切比雪夫不等式
任意分布,只要有均值和方差,取一个值就能得到这个值右边的面积不大于求出的值。把切比雪夫不等式当约等式,就能得到一个差不多的值(t必须在均值的右边,在左边就不准)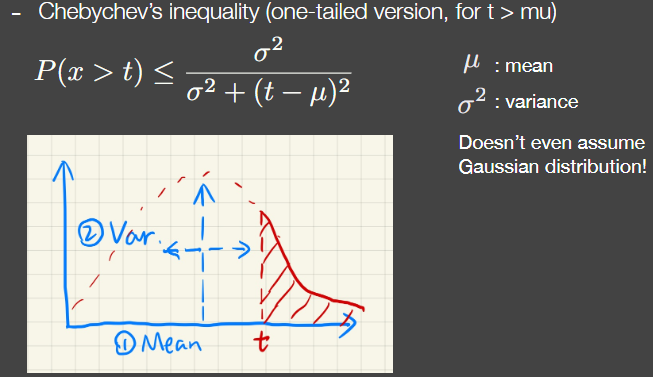
省流:
- 通过生成shadow map和square-depth map得到期望值的平方和平方值的期望再根据公式 得到方差
- 通过mipmap或者SAT得到期望
- 得到期望和方差之后,作出正态分布 根据切比雪夫不等式近似得到一个depth大于shading point点深度的面积.,也就是求出了未遮挡Shading point的概率,从而可以求出一个在0~1之间的visilibity
- 找平均值:
第一步:
要得到一个范围内遮挡物的平均深度。要把所有texels都得采样一遍很耗时
遮挡物的平均深度定义为$Z_occ$ ,不是遮挡物的平均深度定义为$Z_unocc$
平均深度 = 遮挡物所占比例 * 遮挡物的平均深度 + 非遮挡为所占比例 * 非遮挡平均深度
遮挡物所占比例和非遮挡为所占比例依旧可以用切比雪夫不等式近似得成,把非遮挡物的深度假设为当前shaderpoint的深度,就能得到遮挡物的平均深度。这样就不需要采样每个texels
VSSM 大胆假设 接受平面是曲面或者与光源不平行的时候就会出问题 主流还是PCSS
cons: 漏光 不连续阴影
Moment shadow mapping (MSM)
VSSM 的假设有时并不准确 MSM解决分布不为正态分布的问题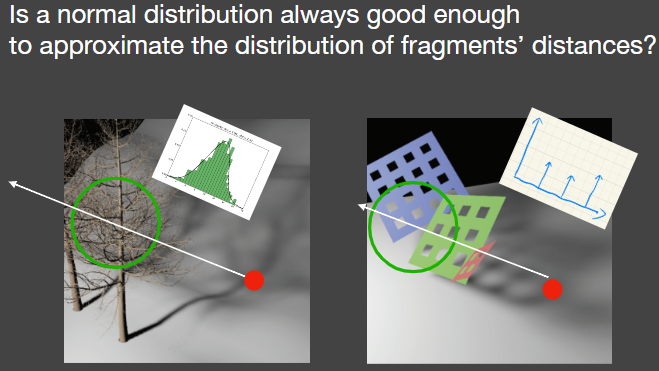
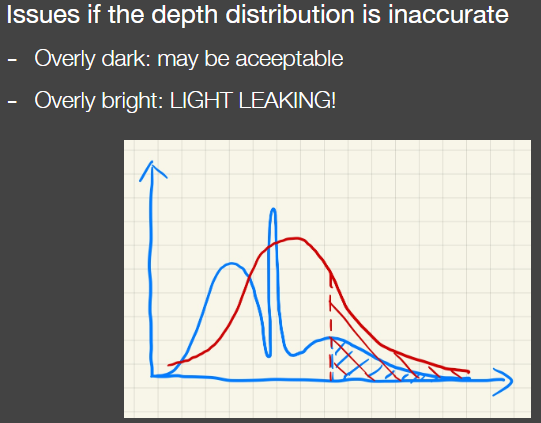
只有三个片的遮挡的情况下,那么深度的分布就在这三个遮挡度深度周围,形成了三个峰值
不是正态分布强行按正态分布算就会出现漏光和过暗的结果。在阴影的承接面不是平面的情况下也会出现阴影断掉的现象 light leaking
- solution:
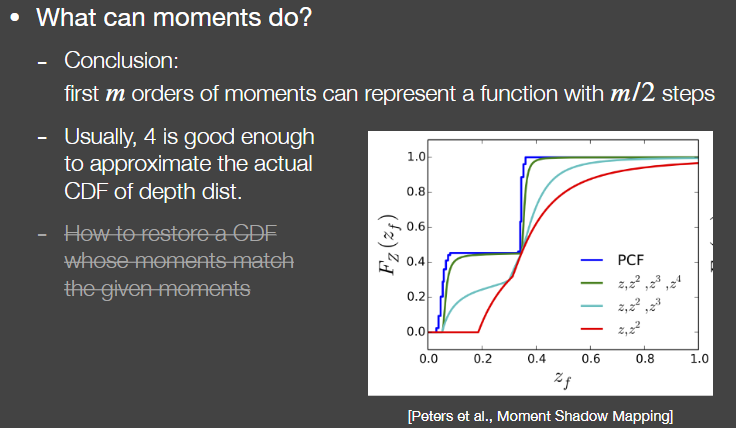
要描述的更准确,就要使用更高阶的moment(矩),矩的定义有很多,最简单的矩就是记录一个数的次方,所以VSSM就等于用了前两阶的矩。这样多记录几阶矩就能得到更准确的结果 (类似泰勒展开?)
如果保留前M阶的矩,就能描述一个阶跃函数,阶数等2/M,就等于某种展开。越多的阶数就和原本的分布越拟合。一般来说4阶就够用
Distance field soft shadows (DFSS)
SDF
空间任何一个点到物体表面的最小距离,通过数值正负得到是否在物体内部,就是距离场distance function(SDF 有向距离场)。SDF引用在3D场景的话,需要存储一整个3d格子,这样存储开销就很大
当距离0为实,即可认为是物体的边界,SDF可以很准确地反应物体的边界。几何转换SDF的时候,可以很好地把几何进行过渡
- usages:
- 字体渲染
- 几何形变(GAMES101)
- Ray marching
当我们已经获得整个场景里物体SDF,有一根光线需要和SDF定义的物体隐含表面进行求交,最简单的求交方式就是sphere tracing。当光线于任意一点时,通过sdf就能得出一个安全范围内,这个光线在安全距离可以任意地向前走,在到达新的点的时候又可以通过sdf确定新的安全距离。当这个光线的距离场足够小的时候就可以很方便地和物体表面求交,或者这个光线走的足够远的时候就可以放弃这个光线的追踪
- soft shadows
通过sdf可以获得大概有多少的范围被挡住,将安全距离的概念进行延伸,在任意一点通过sdf可以获得一个安全角度。把shading point和光源相连,所得到的安全角度越小,被遮蔽的可能越高,就可以认为安全角度越小,阴影越黑,安全角度够大就视为不被遮挡没有阴影 也就越趋近于软阴影
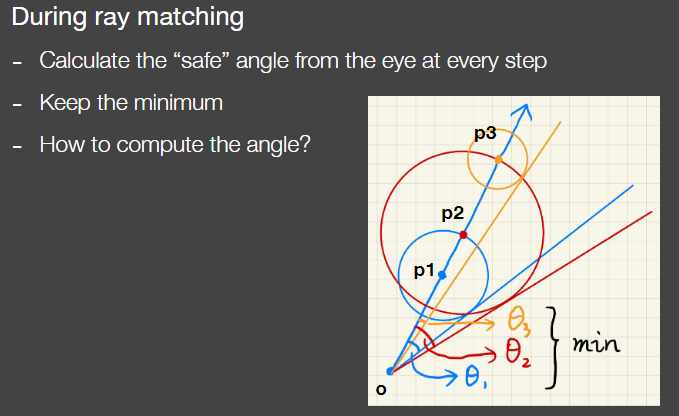
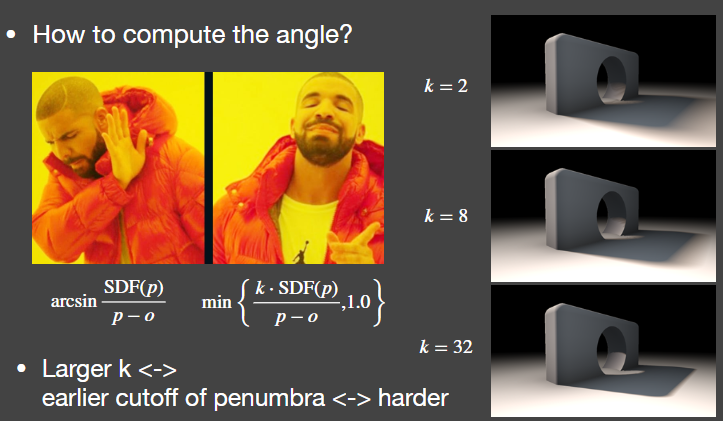
在光线延伸的路径上,每个点都有一个安全距离,光源和安全距离的点所形成的圆的切线和光线能形成夹角,角度最小的夹角就是安全。但这么算的复杂度太高,只要sdf长度除以光线走过的距离乘一个值k,再限定到1以内,就能得到遮挡值,而k的大小就能控制阴影的软硬程度
SDF用来做软阴影的速度非常快,而且质量很高,但是在存储上的消耗非常大,而且生成SDF的花的时间也要很久,SDF是预计算,在有动态的物体的情况就得重新计算SDF SDF生成的物体表面不太好贴纹理

